Convective heat transport in nanofluids

Participants

AM 3

• Eberhard Bänsch
• Sara Faghih-Naini

Description

In the recent past, nanofluides were frequently used as cooling fluids because of their very good heat transfer properties, e.g. for electronics cooling. Consequently, many numerical models for convective heat transport in nanofluids have been developed. One of these is the nowadays frequently used one of Buongiorno.
In this project, a slightly modified, thermodynamically consistent model based on the aforementioned one was is investigated numerically and theoretically.

Results

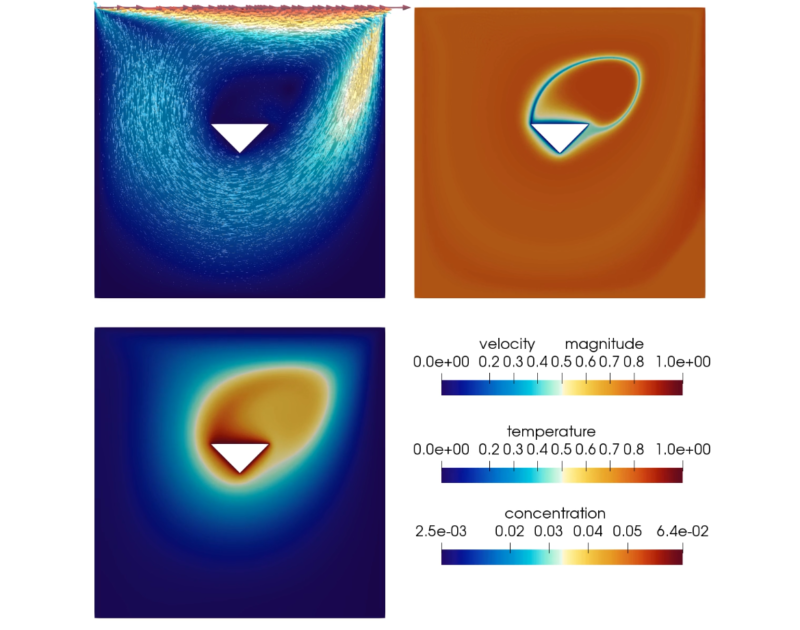
Numerical simulations of a flow through a pipe where an in-time periodic heat flux was applied to one side were performed, furthermore a lid-driven cavity example with a triangular heat source in the middle was investigated.
The simulation results show first of all that nanofluids with higher nanoparticle concentrations have enhanced cooling properties. Furthermore, thermophoresis, i.e. the diffusion of particles under the effect of a temperature gradient, supports the enhanced cooling which can be explained by the following mechanism: an enhanced reduction of nanoparticle concentration close to the wall leads to a reduced viscosity close to the wall which in turn increases the velocity in that area and leads to an increased convective heat transport.
In the theoretical part, fixed point and mollification methods were used to show the existence of a weak solution to the stationary problem.