Higher order time discretization for free surface flows (2010-2016)

DFG Priority Programme 1506: Transport Processes at Fluidic Interfaces

Participants in this project at AM3

• Eberhard Bänsch
• Stephan Weller
• Martin Weismann

Aims of the project

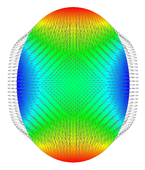Oscillating droplet: A simple example of capillary flow that is used to study different time discretization methods

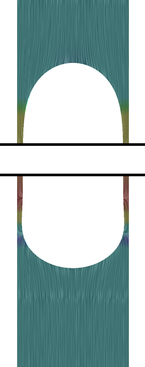Taylor Bubble: Bubble in small container that is used to compare experimental measurements to simulation results

The fundamental problems in the numerical approximation of multiphase systems, or more generally speaking, in the treatment of flows with capillary free boundaries are the representation of the free surface, evaluating the curvature, handling of discontinuities, most importantly the pressure jump, and time discretization strategies for the decoupling of flow computation and geometry.

While for the first three items there exists a vast literature and many techniques developed over the last two decades, the last problem of how to efficiently treat the time discretization has been widely ignored. The majority of the existing approaches just decouple the flow field from the geometry by a simple segregated approach, i.e. evaluating the geometric quantities from the previous time step. These strategy leads to a) a severe capillary CFL condition and b) is of first order in time at most. Existing semi-implicit discretizations exist that overcome problem a), but are still first order only and rather dissipative in certain situations.

To validate the simulation results, measurements from experimental groups were used as well as results from other numerical groups.

In the scope of this project, different at least partly implicit time discretization methods were implemented that are unconditionally stable and only minimally dissipative. These methods will be carried over to more flexible geometric situations (large grid deformations) using a new geometry treatment.