Temporal Multiscale Methods for an Atherosclerosis Model
Temporal Multiscale Methods for an Atherosclerosis Model
Participants
AM 3
Description
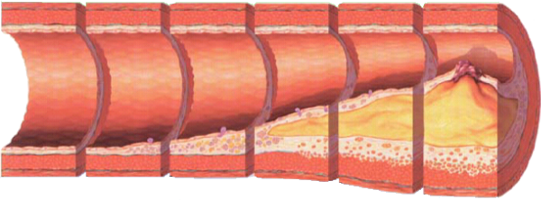
Phases of atherosclerosis, image licensed under CC BY-SA 3.0, original
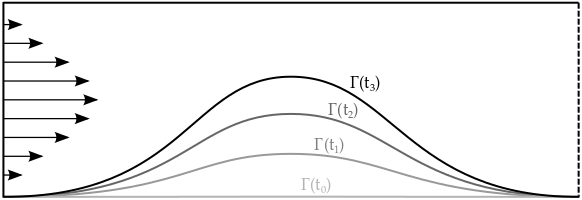
Atherosclerosis is a disease where, through a chain of biological and mechanical processes, plaque forms and grows in artery walls. One aspect of plaque growth models are the stresses excerted by the pulsating blood flow on the wall surface. A direct numerical simulation of such models is infeasible over realistic time spans for plaque growth: Every single heart beat had to be simulated over a span of months or years.
The goal of this project is the rigorous derivation of plaque growth models which allow numerical simulation over long time spans. This is done by considering the original problem as a singularly perturbed system of partial differential equations with periodic blood inflow. By rigorous derivation of a limit problem and quantification of the convergence rate in the perturbation parameter we arrive at a model which is a good approximation of the original problem but allows for numerical simulations over realistic time spans. Behavior and properties of this system are studied numerically.