A discontinuous Galerkin method for the subjective surfaces problem

Participants

AM 3

• Michael Fried

AM 1/AM

• Vadym Aizinger
• Leon Bungert

Description

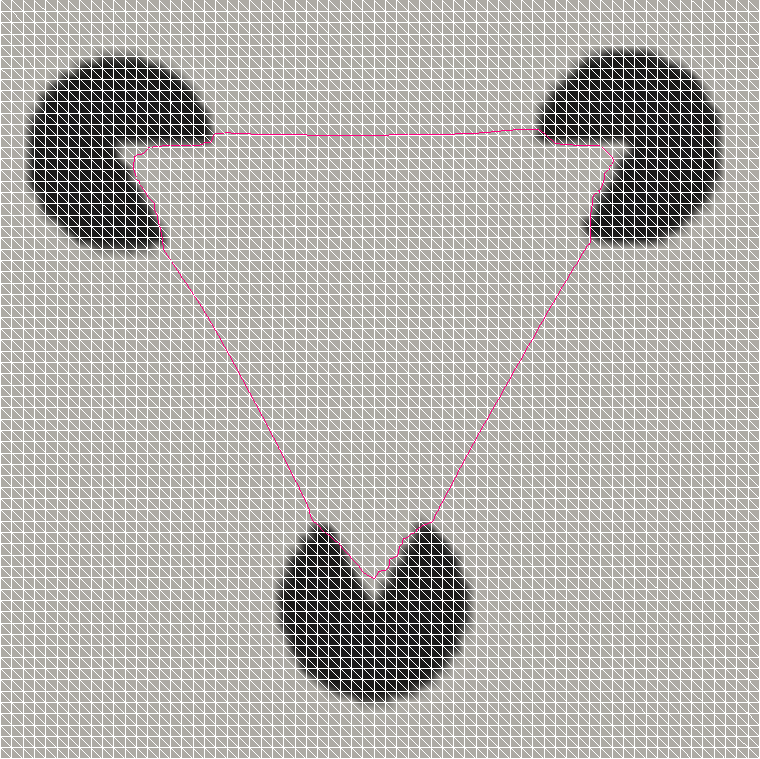
One of the fundamental problems in image analysis is segmentation, i.e., identifying different regions in a given image. Depending on the particular task, these regions may differ by various properties such as color or gray level, texture, noise level, etc.; they also could be defined by their boundaries correlated with some more or less discernible edges. Often, the regions of interest correspond to some object that has to be detected in the image. Presence of noise, covered object parts, or destroyed image information may lead to rather irregular or interrupted edges. Similarly, subjective contours tests known from psychology such as Kanizsa’s triangle are missing large parts of the object’s edges. The latter problem is called ‘subjective surfaces problem’.

This project formulates and evaluates the local discontinuous Galerkin method for the subjective surfaces problem based on the curvature driven level set equation. A new mixed formulation simplifying the treatment of non-linearities is proposed. The numerical algorithm is evaluated using several artificial and realistic test cases and compared to a previous approach of Mikula and Fried using finite elements.

Results

A code verification test with known analytical solution as well as numerical results for several benchmarks show that the LDG method is well suited for subjective surface segmentation and leads to accuracy levels comparable to the finite elements used by Mikula and Fried while avoiding spurious peaks arising in the finite element approach. Piecewise linear DG approximations compare favorably to piecewise constant ones when applied to resolving the object edges on coarse grids. The applicability of the method for medical data was shown as well.

The results obtained in the course of this study motivate extending the proposed method for more complex, realistic images and 3D applications. The question of the computational performance of numerical schemes based on the DG framework has to be addressed in future work as well.