Non-newtonian two-phase flow in an industrial filling process

Participants

AM 3

• Eberhard Bänsch
• Ina Schüssler

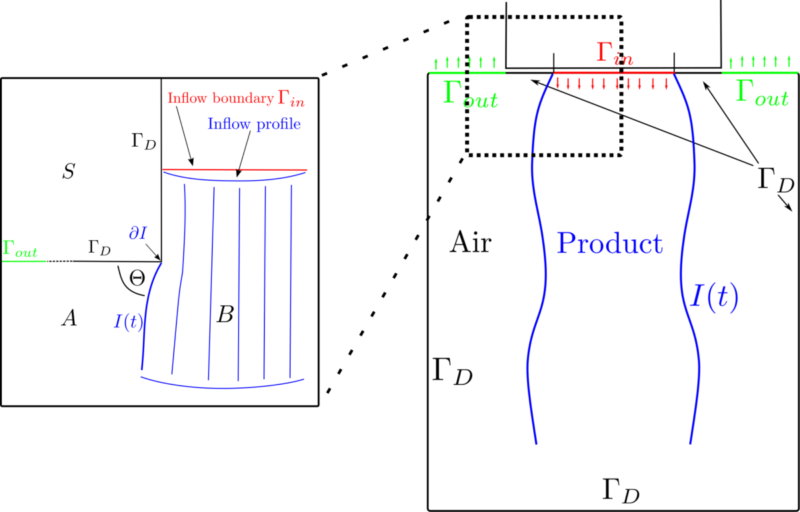
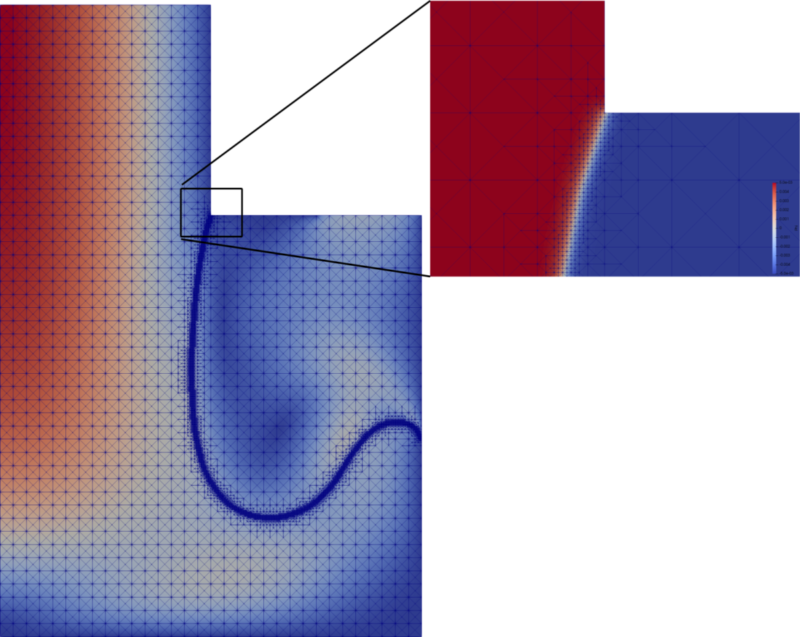
Description

We are developing and implementing a finite element model of a two phase flow. The model includes two phases – one a non-newtonian fluid, the other one air – and the mathematical description of the interface between the phases. The description of the flow is based on the Navier-Stokes equations. The non-newtonian properties are described by the Carreau law, a power law, which allows to model the shear-thinning quality of the fluid.

The levelset method is designed to capture the movement of the interface. We are using an implicit reinitialization technique which is included in the levelset equation by altering the right hand side (following [Bonito]). The accuracy with which the interface is represented depends on a delta-function which depends in turn on the levelset function and the resolution of the grid around the interface. The width of the delta function affects the accuracy of the numerical calculation of surface tension.

The filling process takes place on a moving domain. This causes the necessity to move the grid and -if the movement is too large- remesh the domain. The grid movement is represented in the equations using ALE-transformation.

References

• A. Bonito, J.-L. Guermond, S. Lee (2016). Numerical Simulations of Bouncing Jets. Numerical Methods in Fluids, 80: 53-75.