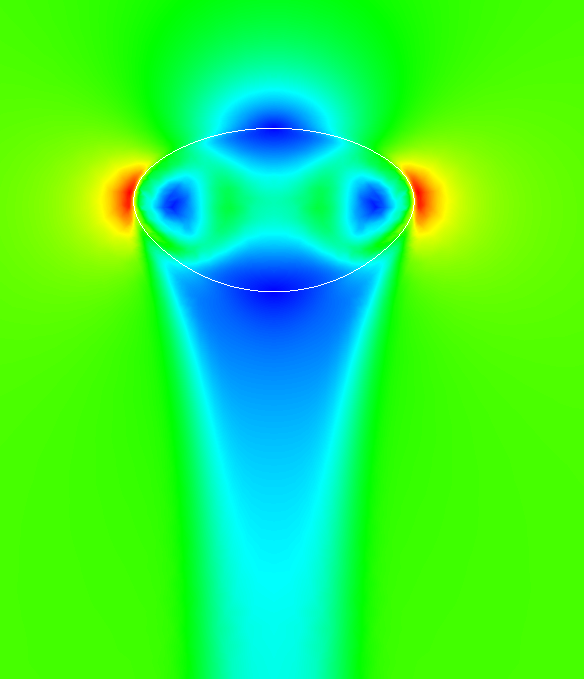
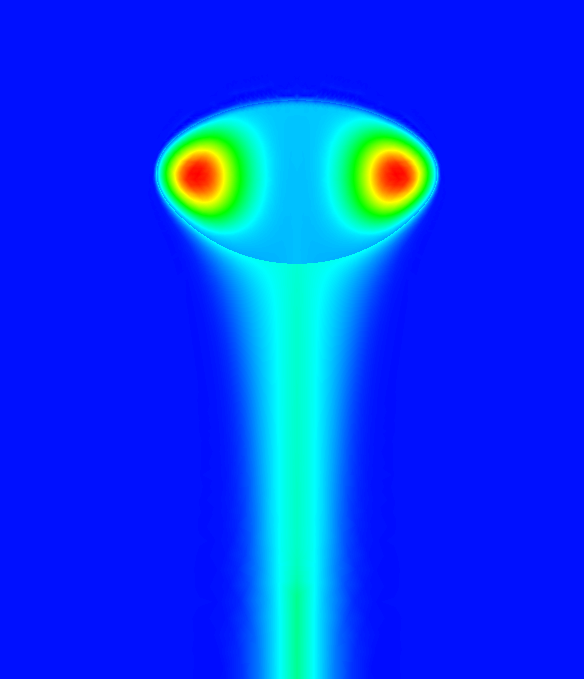
Marangoni convection
Participants
AM 3
- Eberhard Bänsch
- Kathrin Bäumler
External
- A. Paschedag
- M. Wegener
Application
In liquid/liquid extraction processes the objective is to extract a solutant that is contained in one liquid phase to another, usually immiscible liquid phase. For this purpose one phase is dispersed into the other, and the mass transfers across the interface of these drops. Since liquid/liquid extraction is an important part of many process plants, there is a large interest to improve extraction performance, and efficiently design extraction columns.
Predictions of retention times, mass transfer coefficients, the influence of surfactants, etc. are not always satisfying, especially when considering Marangoni-convection. As analytical description is often unavailable, and since experiments are costly, numerical simulations are constantly improved to face the difficulties of these complex two-phase flow problems.
Mathematical model
The two-phase flow with mass transfer is modelled by the Navier-Stokes equations for immiscible, incompressible Newtonian fluids in the bulk phases Ωj. Mass transfer is modelled via a convection-diffusion equation.
- ρj ∂t uj + ρj ( uj ·∇) uj -Δ uj +∇ pj = ρj fj
- ∇· uj = 0
- ∂t cj +( uj ·∇) cj -Δ cj = 0
The unknowns u,p,c are the velocity, pressure and concentration. The subscript j denotes the respective phase ( d for the dispersed (drop) phase or c for the continuous phase). f is the given right hand side of the Navier-Stokes equations, describing external forces (here: gravity). Given material parameters are density ρ , dynamic viscosity μ, and the diffusion coefficient D.
The interfacial conditions on the interface Γ have the form:
- [u] = 0
- [σν] = γκν- ∇S γ(c)
- [D∇c·ν] = 0
- cc = H cd
Here, σ=μ(∇u+ (∇ u) Τ )-pI denotes the stress tensor, ν the normal vector on Γ pointing from Ω c to Ω d , κ is the sum of the principal curvatures, with the convention κ>0 if Ω d is convex. V Γ denotes the velocity of Γ in direction of ν and ∇ s the surface gradient. The brackets [⋅] notate the jump of a quantity across Γ , and H is called partition quoefficient or Henry coefficient.
The equation containing the surface gradient couples the flow field with the solute concentration, resulting in concentration-induced convective patterns, called Marangoni-convection.
Numerical method
The two-phase flow problem is solved with the code NAVIER, augmented with the following features:
- Subspace Projection Method, an efficient implementation of the interface conditions, suited for a simultaneous solving of the two phases.
- SUPG – Streamline Upwind Petrov Galerkin formulation. A method used for an enhanced stability of the convection-dominated mass transfer problem.
- Grad-Div stabilization for the Navier-Stokes equation.