Modern approaches to solving the Full-Stokes problem in the context of ice sheet modeling

Participants

AM 3

• Eberhard Bänsch
• Luca Wester

Description

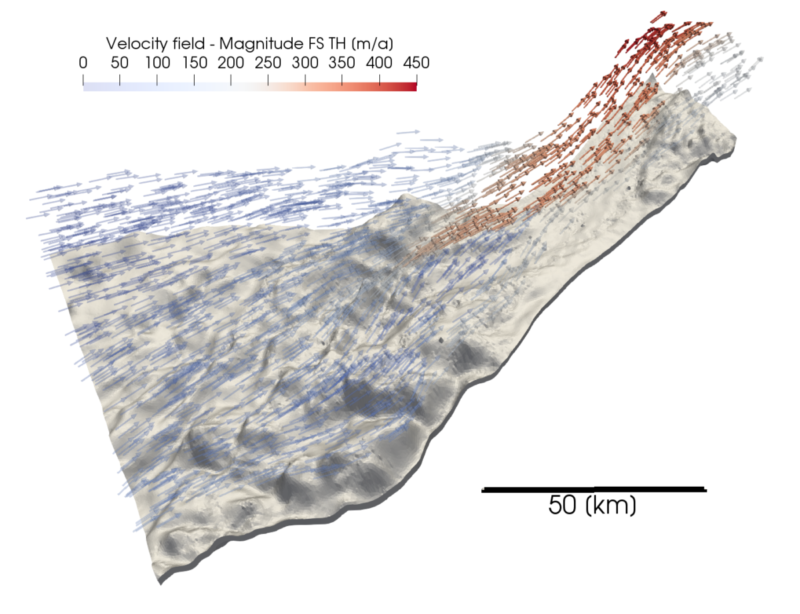
A significant part of the global average sea level rise can be attributed to the melting of the cryosphere, in particular the continental-scale ice sheets in Greenland and Antarctica. Observations over recent decades show that both ice sheets lose mass at an accelerated rate, which yields a need for accurate and reliable predictive simulations. Current applications often reduce the full underlying set of physical balance equations (the Full Stokes system, FS) to simplified equations, as the complexity of the FS system and the inherently nonlinear viscosity make them quite challenging to solve even on high-end machines. In return, various physical properties of the glaciers get neglected. This project aims to combine the disciplines of glaciology and mathematics, in order to accurately represent the physical properties of glaciers by solving the FS system with state-of-the-art mathematical solvers.

Results

We use the open source Ice Sheet System Model (ISSM) in all our simulations. In its original implementation, ISSM used either direct solvers (MUMPS) or applied iterative solvers to the full block matrix in saddle point structure. Direct solves suffers from high storage requirement and long runtimes, whereas the iterative solvers often lead to instabilities in practical applications, especially in cases with elements of aspect ratio. To combat this, we implemented a Schur-complement based conjugate gradient (CG) method into ISSM, which shows promising results in terms of stability, even at bad aspect ratios.