Software
Software
This website provides an overview on software that has been developed for research and teaching. Some of the projects can be assessed via gitlab (including codes):
https://repo.mi.uni-erlangen.de/imaging/code/public/
SiMRX
SiMRX is a MRX simulation toolbox written in MATLAB for simulation of realistic 2D and 3D Magnetorelaxometry (MRX) setups, including coils, sensors and activation patterns. (mehr Informationen)
flexBox
FlexBox is a flexible MATLAB toolbox for finite dimensional convex variational problems in image processing and beyond. (mehr Informationen)
helperFiles
The helperFiles package provide nice little tools in MATLAB to visualize image and volume data, to create formatted output, as well as other small helpful programs. (zum Repository)
R I C H Y 1D
Abstract
RICHY1D is a simulation software for physical transport problems modelled by partial differential equations.
- works in 1 spatial dimension,
- simulates time and space dependent problems,
- includes the solution of inverse problems to identify model parameters
- … and provides many more features for mathematicians and engineers, described within this manual.
RICHY1D’s main purpose is to support the evaluation of soil RemedIation and RIsk assessment scenarios. A typical situation of interest is a Contaminated site, where the spreading of CHemicals in the soil exhibits a Hazard for the environment. Model equations for (un-)saturated water flow and for solute transport were the first problems of HYdrology, numericallY
solved with RICHY1D.
“The application of natural attenuation as a site remediation strategy depends essentially on the reliable prediction of the migration of the contaminant plume.
[RICHY1D is] a one-dimensional simulation tool that is capable of handling a variety of complex scenarios predicted to be of interest in site remediation problems. The implementation of the different components is organized in a modular structure that facilitates arbitrary extensions of the incorporated models and enables the model components to be combined. Efficient, robust numerical techniques (e.g. hybrid mixed finite elements) are embedded in a menu driven, user-friendly environment to serve hydrogeologists or engineers without profound knowledge of the mathematical theory. The software is suitable for Unix workstations as well as inexpensive personal computers. The model components include reactive solute transport (with diffusion, dispersion, advection and sorption) and single- as well as two-phase flow in the saturated and the vadose zone. The underlying models contain non-standard effects that enable the simulation of a large variety of relevant support strategies for natural attenuation.”
[E. SCHNEID, A. PRECHTEL, P. KNABNER. A Comprehensive Tool for the Simulation of Complex Reactive Transport and Flow in Soils. Land Contamination & Reclamation, 8(4):357-365, 2000.]
The following processes can be modelled and simulated with RICHY1D:
– Water flow in the saturated and vadose zone including preferential flow
– Reactive solute transport with diffusion, dispersion, advection and sorption including equilibrium isotherms and multiple site kinetics
– Carrier facilitated transport
– Biodegradation with biomass dynamics, multiple monod kinetics and inhibition terms
– Coupled water and surfactant transport
– Heat transport including temperature dependant degradation reactions for solutes
– General stoichiometric reaction kinetics
– Mineral dissolution and precipitation
The majority of the above problem classes can be used with inverse modelling routines to identify unknown parameters through various parameter identification algorithms. On the basis of experimental data, e.g. the breakthrough curve of a column experiment, unknown model parameters are identified even simultaneously.
Example simulations for each problem class lead to the corresponding settings.
The underlying numerical algorithms are state-of-the-art techniques of modern mathematics, including mixed hybrid finite element methods, adaptive grid strategies, fully implicit coupling of transport and reaction problems and more where necessary.
RICHY1D is used interdisciplinarily by research institutes in mathematics and the geo sciences, consultants, and authorities as well.
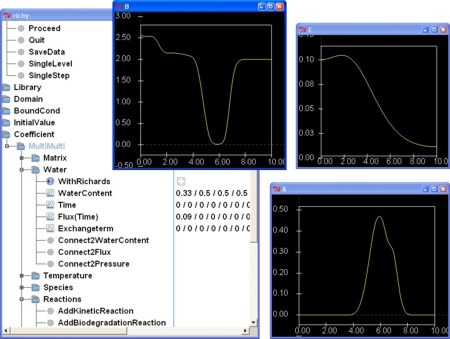
GUI
RICHY1D’s GUI is built with Tcl/Tk to maintain portability. Have a look at the following screenshot done on a Windows7 OS:
Documentation
The entire documentation is available as a linked pdf. The links are organized in a way that it can be used similar to a web page — by clicking the section- or equation names etc. and using the back button — or as a printable book as the links refer to pages. Manual RICHY1D.pdf
RICHY 2D/3D
See also below.
Software Richy2D/3D
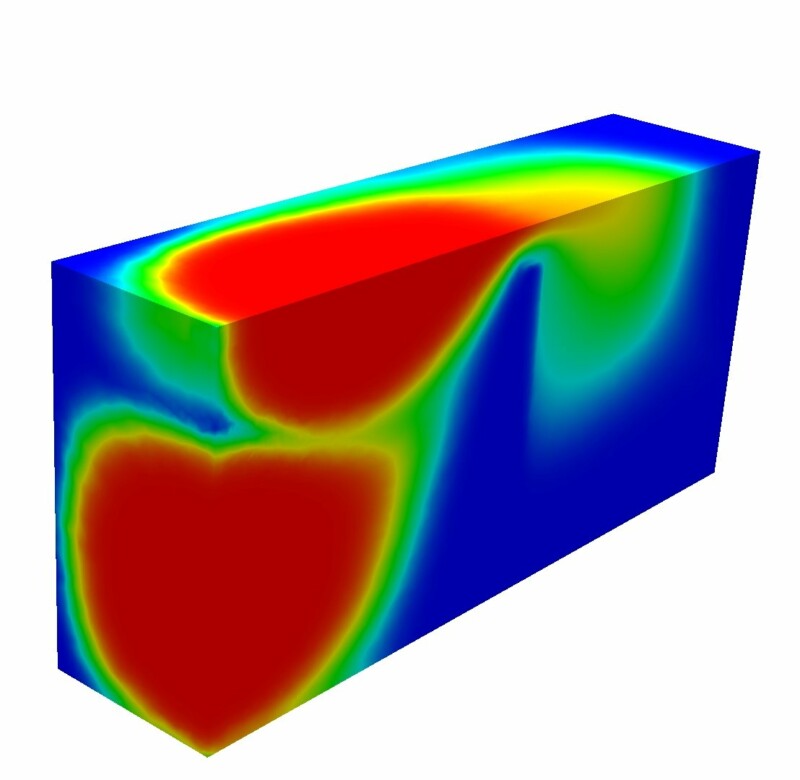
The Software Richy2D/3D solves reactive transport problems in two or three spatial dimensions. The system consists of PDEs for the concentrations of the mobile species and ODEs for the concentrations of immobile species. Reactions can be kinetic and/or equilibrium. If equilibrium reactions are involved, algebraic equations are coupled to the PDE-ODE-system. The groundwater flow can either be given or be computed through the Richards equation.
The software is programmed using M++. It is running on parallel computers. The definition of the scenario and the choice of numerical parameters/algorithms is done by a script-file; a graphical user interface is not available.
Richy2D/3D is based on the global implicit approach (one step method). Its development is driven by the intention to apply modern mathematical techniques to geoscientific problems. Richy2D/3D uses a specific model-preserving size reduction technique to reduce the required cpu time. Reactions with minerals are expressed as Complementarity Problems (CPs) and solved by the Semismooth Newton method. For details on the size reduction technique see the following literature. For the CPs and Semismooth Newton see the habilitation thesis and the AWR publication in particular. The software and its solution algorithms have been awarded in an international benchmark study for reactive multicomponent transport codes (MoMaS) as the most innovative work giving very accurate results while significantly reducing computation times (see also the Comput. Geosc. publications).
- Hoffmann, J., Kräutle, S., Knabner, P.: A general reduction scheme for reactive transport in porous media, Comput. Geosci., 16, p.1081-1099, 2012.
DOI: 10.1007/s10596-012-9304-4
Springer-Link Online First
(Preprint No. 353 of the Preprint Series of the Institute for Applied Mathematics, ISSN 1435-5833, 2012, pdf.) - Kräutle, S.: The semismooth Newton method for multicomponent reactive transport with minerals, Advances Water Res. 34, p.137-151, 2011. doi: 10.1016/j.advwatres.2010.10.004
(preprint) (link to article) - Carrayrou, J., Hoffmann, J., Knabner, P., Kräutle, S., de Dieuleveult, C., Erhel, J., Van der Lee, J., Lagneau, V., Mayer, K.U., McQuarrie, K.T.B: Comparison of numerical methods for simulating strongly nonlinear and heterogeneous reactive transport problems–the MoMaS benchmark case, Computational Geosciences 14 (3), pp. 483-502, doi: 10.1007/s10596-010-9178-2, 2010.
- Hoffmann, J., Kräutle, S., Knabner, P.: A Parallel Global-Implicit 2-D Solver for Reactive Transport Problems in Porous Media based on a Reduction Scheme and its Application to the MoMaS Benchmark Problem, Computational Geosciences 14 (3), pp. 421-433, 2010, doi: 10.1007/s10596-009-9173-7, 2010
- Kräutle, S., General multi-species transport problems in porous media: Efficient numerical approaches and existence of global solutions, Habilitation thesis, University of Erlangen, 2008.
gzipped-PS-Version PDF-Version - Kräutle, S., Knabner, P.: A Reduction Scheme for Coupled Multicomponent Transport-Reaction Problems in Porous Media: Generalization to Problems with Heterogeneous Equilibrium Reactions, Water Resour. Res., 43, W03429, doi:10.1029/2005WR004465, 2007.
PS-Version (490kB), PDF-Version (290kB) - Kräutle, S., Knabner, P.: A new numerical reduction scheme for fully coupled multicomponent transport-reaction problems in porous media, Water Resour. Res., 41, W09414, doi:10.1029/2004WR003624, 2005.
- Hoffmann, J.: Ein Entkopplungsverfahren für Systeme von Transportreaktionsgleichungen in porösen Medien: Algorithmische Umsetzung und Simulation realistischer 2D-Szenarien, Diploma thesis, University of Erlangen, 2005 (gzipped PostScript 6.2 MB, PDF 3.2 MB)
For M++ see:
- Wieners, W., Distributed point objects, A new concept for parallel finite elements, in Domain decomposition methods in science and engineering, Lecture notes in computational science and engineering, Vol. 40, R. Kornhuber, R. Hoppe, J. Periaux, O. Pironneau, O. Widlund, and J. Xu (eds.), Springer 2004, pp. 175–183.
Alle Informationen zu dieser Software finden Sie hier.
FESTUNG (Finite Element Simulation Toolbox for UNstructured Grids) |
||||||||||||||||||||||
|
FESTUNG – A MATLAB / GNU Octave toolbox for the discontinuous Galerkin method
FESTUNG is an Open Source toolbox for the discontinuous Galerkin method on unstructured grids, written in Matlab / GNU Octave. It is primarily intended as a fast and flexible prototyping platform and testbed for students and developers. It relies on fully vectorized matrix/vector operations to deliver optimized computational performance combined with a compact, user-friendly interface and a comprehensive documentation.
Current features
A selection of the current set of features of FESTUNG includes
- Generic problem description and coupling framework.
- Unstructured 1D and 2D (triangular, trapezoidal) meshes.
- (L)DG/HDG discretizations up to fourth order (with hierarchichal polynomial basis functions).
- explicit SSP Runge-Kutta (up to 3rd order) and implicit DIRK scheme (up to 4th order) time discretization.
- High-order hierarchical vertex-based slope limiters.
- Fully vectorized assembly.
- VTK– and Tecplot-compatible output.
- Advection– and diffusion-type operators readily available.
Getting started
To start using FESTUNG, clone our public GitHub repository and run one of the included model problems, as described in the documentation.
Source code repository
Up-to-date versions of FESTUNG are available in our public Github repository.
Preprints and Publications
A detailed and continuosly updated documentation of all routines can be found under www1.am.uni-erlangen.de/FESTUNG.
Publications describing FESTUNG or showing its application are listed below:
- A preprint of the first paper, describing an older code version, is available from arXiv and we provide the codes described there as a gzip-archive.
- Our first paper FESTUNG: A MATLAB/GNU Octave toolbox for the discontinuous Galerkin method, Part I: Diffusion operator describes the basic data structures and discretization techniques.
The code corresponds to version 0.1 of FESTUNG. - Our second paper FESTUNG: A MATLAB/GNU Octave toolbox for the discontinuous Galerkin method, Part II: Advection operator and Slope Limiting describes the discretization of a hyperbolic operator and slope limiting techniques.
The code corresponds to version 0.2 of FESTUNG.
A preprint of the paper, describing code version 0.2-beta.1, is available on arXiv. - Our third paper “FESTUNG: A MATLAB/GNU Octave toolbox for the discontinuous Galerkin method, Part III: Hybridized discontinuous Galerkin (HDG) formulation” (submitted to CAMWA).
A preprint of the paper, describing code version 0.3-beta.1, is available on arXiv. - A poster at SIAM Geosciences 2017 outlining the features and concepts of FESTUNG.
Data visualization
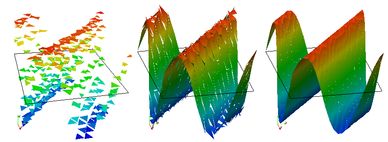
FESTUNG writes VTK- and Tecplot-files with the computed solution that can be visualized, e.g., using Paraview or Tecplot 360.
UTBEST3D (University of Texas Bays and Estuaries Simulator — 3D) |
||||||||
|
UTBEST3D (University of Texas Bays and Estuaries Simulator — 3D)
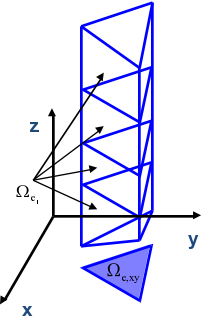
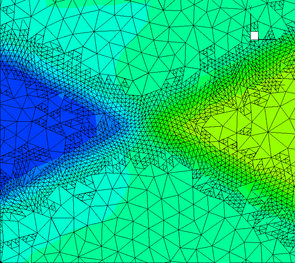
The numerical solution algorithm in UTBEST3D considers the system of hydrostatic primitive equations (1) with a free surface. A prismatic mesh (Fig. 1) is obtained by projecting a given triangular mesh in the vertical direction to provide a continuous piecewise linear representations of the topography and of the free surface. The vertical columns are then subdivided into layers. If a bottommost prism is degenerate, it is merged with the one above it. Due to the discontinuous nature of the approximation spaces, no constraints need to be enforced on the element connectivity. Hanging nodes and mismatching elements are allowed and have no adverse effects on stability or conservation properties of the scheme. This flexibility with regard to mesh geometry is exploited in several key parts of the algorithm: vertical mesh construction in areas with varying topography (Fig. 4), local mesh adaptivity (Fig. 2), wetting/drying (Fig. 3).
partial_t {bf u}_H +nabla cdot left( {bf u}_H {bf u} – D_{bf u} nabla{bf u} right) + nabla_H P -f_C {bf k} times {bf u}_H =0
partial_t T + nabla cdot left({bf u} T – D_T nabla T right) = 0
partial_t S + nabla cdot left({bf u} S – D_S nabla S right) = 0
partial_t xi + nabla_H cdot int_{z_b}^{xi} {bf u} dz =0hspace{45mm}(1)
nabla cdot {bf u} =0
partial_z P= – frac{rho}{rho_0}g
rho = rho(T,S,z)
nabla_H = (partial_x,partial_y), {bf k} = (0,0,1)^T, D_{X, X in {{bf u},S,T}} – eddy viscosity/diffusivity, xi – free surface elevation, z_b – bathymetry, {bf u}= (u,v,w) – velocity, {bf u}_H= (u,v), T – temperature, S – salinity, P – pressure, rho – density, rho_0 – reference density, g – gravity acceleration, f_C – Coriolis coefficient.
Our DG discretization is based on the local discontinuous Galerkin method (Cockburn, Shu, 1998) that represents a direct generalization of the cell-centered finite volume method, the latter being just the piecewise constant DG discretization. One of the features of this method is a much smaller numerical diffusion exhibited by the linear and higher order DG approximations compared to the finite difference or finite volume discretizations. The method guarantees the element-wise conservation of all primary unknowns including tracers, supports an individual choice of the approximation space for each prognostic and diagnostic variable, demonstrates excellent stability properties, and possesses proven local adaptivity skills (Fig. 2).
UTBEST3D is written in C++ to provide clean interfaces between geometrical, numerical, computational, and communication parts of the code. The object-oriented coding paradigm is designed to enable a labor efficient development lifecycle of the model. The programming techniques were carefully chosen and tested with the view of guaranteeing a smooth portability to different hardware architectures, operating systems, compilers, and software environments; the package relies on no external libraries in the serial configuration and only makes use of METIS (Karypis, Kumar, 1999) grid partitioning library in the parallel configuration.
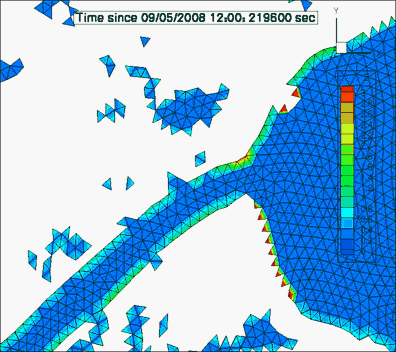
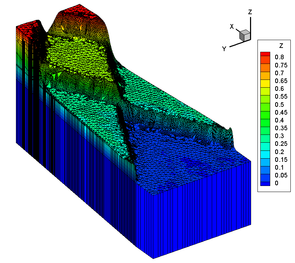
Wetting/drying simulation of a storm surge during hurricane Ike. Visible fractionally subdivided elements at the wet/dry interface.
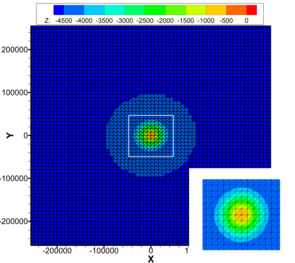
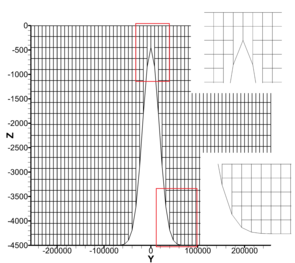
Geometry and mesh of the steep seamount test case. Bathymetry and horizontal mesh, vertical mesh.
Bibliography
- Vadym Aizinger, A discontinuous Galerkin method for two- and three-dimensional shallow-water equations, PhD Dissertation, THE UNIVERSITY OF TEXAS AT AUSTIN, 2004.
- V. Aizinger, C. Dawson, The local discontinuous Galerkin method for three-dimensional shallow water flow, Computer methods in applied mechanics and engineering, 196, 734-746, 2007.
- B. Cockburn and C.-W. Shu, The local discontinuous Galerkin method for time-dependent convection-diffusion systems, SIAM J. Numer. Anal. 35, 2440-2463, 1998.
- C. Dawson, V. Aizinger, A Discontinuous Galerkin Method for Three-Dimensional Shallow Water Equations, Journal of Scientific Computing, 22, 245-267, 2005.
- G. Karypis and V. Kumar, A fast and high quality multilevel scheme for partitioning irregular graphs, SIAM Journal on Scientific Computing, 20(1), 359-392, 1999.
EconDrop3D |
||||||
|
EconDrop3D
The software package EconDrop3D provides implementations of stable schemes for the following applications:
Diffuse interface models for two-phase flow of incompressible liquids with general mass densities.
 |
 |
 |
 |
- Grün, G. & Klingbeil, F.: Two-phase flow with mass density contrast: stable schemes for a thermodynamic consistent and frame-indifferent diffuse-interface model. Journal of Computational Physics, Elsevier, 2014, 257, Part A, 708-725.
- Grün, G.: On convergent schemes for diffuse interface models for two-phase flow of incompressible fluids with general mass densities. SIAM Journal on Numerical Analysis, 2013, 51, 3036-3061.
- Aland, S.; Boden, S.; Hahn, A.; Klingbeil, F.; Weismann, M. & Weller, S.: Quantitative comparison of Taylor flow simulations based on sharp-interface and diffuse-interface models. International Journal for Numerical Methods in Fluids, 2013, 73, 344-361.
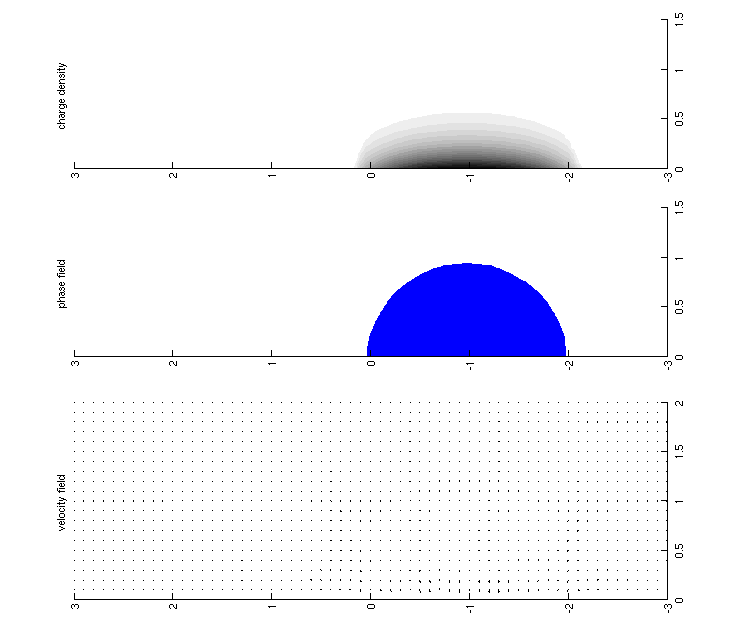
Diffuse interface models for dynamic electrowetting and other electrokinetic phenomena
 |
 |
 |
 |
 |
 |
 |
 |
- Eck, C.; Fontelos, M. A.; Grün, G.; Klingbeil, F. & Vantzos, O.: On a phase-field model for electrowetting. Interfaces and Free Boundaries, 2009, 11, 259-290.
- Campillo-Funollet, E.; Grün, G. & Klingbeil, F.: On Modeling and Simulation of Electrokinetic Phenomena in Two-Phase Flow with General Mass Densities. SIAM Journal on Applied Mathematics, 2012, 72, 1899-1925.
- Klingbeil, F.: On the numerics of diffuse-interface models for two-phase flow with species transport. Friedrich-Alexander-Universität Erlangen-Nürnberg, 2014.
Micro-Macro-models for two-phase flow of dilute polymer solutions

-
- Model based on non-linear coupling of a momentum equation, a Cahn-Hilliard equation and a Fokker-Planck equation,
- Simulation by Stefan Metzger
Thin-film equation

- Non-negativity preserving numerical scheme,
- see Wetting Kaleidoscope for more information.
- Becker, J.; Grün, G.; Blossey, R.; Jacobs, K.; Mantz, H.; Mecke, K. R. & Seemann, R.: Complex dewetting scenarios captured by thin film models. Nature Materials, 2003, 2, 59-63.
- Becker, J.: Numerische Simulation der Bildung fluider Strukturen auf inhomogenen Oberflächen. Rheinische Friedrich-Wilhelms-Universität, 2005.
Stochastic thin-film equation
- Grün, G.; Mecke, K. & Rauscher, M.: Thin-film flow influenced by thermal noise. Journal of Statistical Physics, 2006, 122, 1261-1291.
Features
- adaptive in space and time,
- Mini-element, Taylor-Hood elements and stabilized P1-P1-elements available in 2D and in 3D for discretization of momentum equation,
- Cartesian and cylindrical framework.