EconDrop3D

The software package EconDrop3D provides implementations of stable schemes for the following applications:

Diffuse interface models for two-phase flow of incompressible liquids with general mass densities.

• Grün, G. & Klingbeil, F.: Two-phase flow with mass density contrast: stable schemes for a thermodynamic consistent and frame-indifferent diffuse-interface model. Journal of Computational Physics, Elsevier, 2014, 257, Part A, 708-725.
• Grün, G.: On convergent schemes for diffuse interface models for two-phase flow of incompressible fluids with general mass densities. SIAM Journal on Numerical Analysis, 2013, 51, 3036-3061.
• Aland, S.; Boden, S.; Hahn, A.; Klingbeil, F.; Weismann, M. & Weller, S.: Quantitative comparison of Taylor flow simulations based on sharp-interface and diffuse-interface models. International Journal for Numerical Methods in Fluids, 2013, 73, 344-361.

Diffuse interface models for dynamic electrowetting and other electrokinetic phenomena

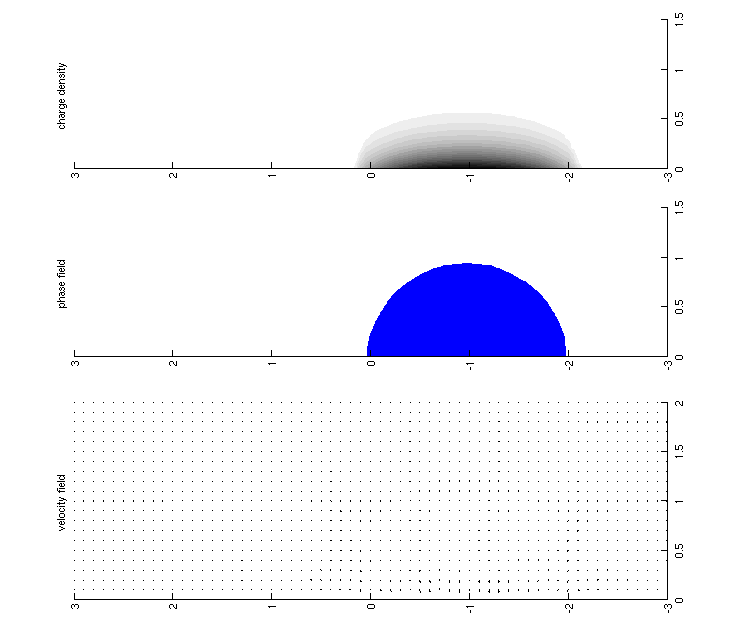• Eck, C.; Fontelos, M. A.; Grün, G.; Klingbeil, F. & Vantzos, O.: On a phase-field model for electrowetting. Interfaces and Free Boundaries, 2009, 11, 259-290.
• Campillo-Funollet, E.; Grün, G. & Klingbeil, F.: On Modeling and Simulation of Electrokinetic Phenomena in Two-Phase Flow with General Mass Densities. SIAM Journal on Applied Mathematics, 2012, 72, 1899-1925.
• Klingbeil, F.: On the numerics of diffuse-interface models for two-phase flow with species transport. Friedrich-Alexander-Universität Erlangen-Nürnberg, 2014.

Micro-Macro-models for two-phase flow of dilute polymer solutions

• • Model based on non-linear coupling of a momentum equation, a Cahn-Hilliard equation and a Fokker-Planck equation,
  • Simulation by Stefan Metzger

Thin-film equation

• Non-negativity preserving numerical scheme,
• see Wetting Kaleidoscope for more information.

• Becker, J.; Grün, G.; Blossey, R.; Jacobs, K.; Mantz, H.; Mecke, K. R. & Seemann, R.: Complex dewetting scenarios captured by thin film models. Nature Materials, 2003, 2, 59-63.
• Becker, J.: Numerische Simulation der Bildung fluider Strukturen auf inhomogenen Oberflächen. Rheinische Friedrich-Wilhelms-Universität, 2005.

Stochastic thin-film equation

• Grün, G.; Mecke, K. & Rauscher, M.: Thin-film flow influenced by thermal noise. Journal of Statistical Physics, 2006, 122, 1261-1291.

• adaptive in space and time,
• Mini-element, Taylor-Hood elements and stabilized P1-P1-elements available in 2D and in 3D for discretization of momentum equation,
• Cartesian and cylindrical framework.