Multicomponent reactive transport

Multicomponent reactive transport in natural porous media
Participants: Serge Kräutle, Nadja Ray, Alexander Prechtel, Raphael Schulz, Fabian Brunner, Matthias Herz, Tobias Elbinger, Ernesto Monaco; formerly Hari Mahato

The modeling of reactive transport problems in porous media leads to large systems consisting of partial and ordinary differential equations, coupled through source terms (e.g., arising from kinetic reactions) and through algebraic equations (coming from very fast, i.e., equilibrium reactions). If mineral precipitation-dissolution reactions are involved, then the system is additionally coupled to a complementarity problem.
Our work has the following main foci:
The modelling of the processes (including mineral precipitation-dissolution, electrostatic forces, the influence of microbia),
the development of efficient and robust numerical techniques for such systems (read more), and
the analysis of such systems, in particular the question of existence of global solutions, which is tackled with fixed point techniques.

Application of our cpu-time saving ‘Reduction Scheme’ (Richy2D/3D) to the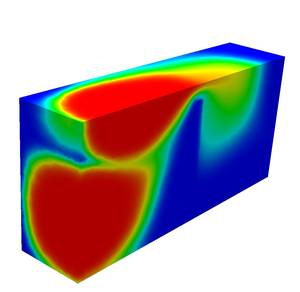
MoMaS Benchmark on Reactive Transport
See:
Carrayrou, J., Hoffmann, J., Knabner, P., Kräutle, S., de Dieuleveult, C., Erhel, J., Van der Lee, J., Lagneau, V., Mayer, U., MacQuarrie, K.T.B.: Comparison of numerical methods for simulating strongly non-linear and heterogeneous reactive transport problems – the MoMaS benchmark case, Comput. Geosci. 14, p.483-502, 2010.

Hoffmann, J., Kräutle, S., Knabner, P.: A parallel global implicit 2-D solver for reactive transport problems in porous media based on a reduction scheme and its application to the MoMaS benchmark problem, Comput. Geosci., 14, p.421-433, 2010.

See here  for the description of the benchmark.
Figure: MoMaS Benchmark on multicomponent reactive transport, our extension of the 2-D setting to 3-D: visualization of the tracer species; flow field computed with mixed finite elements.

 

 

Another Application: Carbon dioxide storage by mineral trapping

We consider a generic (simplified) set of chemical reactions that contains a principal mechanism which may take place in subsurface CO_2 storage sites. It consists of 3 mineral species, 3 sorption sites, 7 aqueous species, and 6 reactions, 3 of them at equilibrium.

Details see: Kräutle, S.: The semismooth Newton method for multicomponent reactive transport with minerals, Advances Water Res. 34, p.137-151, 2011.