FESTUNG
FESTUNG (Finite Element Simulation Toolbox for UNstructured Grids) |
||||||||||||||||||||||
|
FESTUNG – A MATLAB / GNU Octave toolbox for the discontinuous Galerkin method
FESTUNG is an Open Source toolbox for the discontinuous Galerkin method on unstructured grids, written in Matlab / GNU Octave. It is primarily intended as a fast and flexible prototyping platform and testbed for students and developers. It relies on fully vectorized matrix/vector operations to deliver optimized computational performance combined with a compact, user-friendly interface and a comprehensive documentation.
Current features
A selection of the current set of features of FESTUNG includes
- Generic problem description and coupling framework.
- Unstructured 1D and 2D (triangular, trapezoidal) meshes.
- (L)DG/HDG discretizations up to fourth order (with hierarchichal polynomial basis functions).
- explicit SSP Runge-Kutta (up to 3rd order) and implicit DIRK scheme (up to 4th order) time discretization.
- High-order hierarchical vertex-based slope limiters.
- Fully vectorized assembly.
- VTK– and Tecplot-compatible output.
- Advection– and diffusion-type operators readily available.
Getting started
To start using FESTUNG, clone our public GitHub repository and run one of the included model problems, as described in the documentation.
Source code repository
Up-to-date versions of FESTUNG are available in our public Github repository.
Preprints and Publications
A detailed and continuosly updated documentation of all routines can be found under www1.am.uni-erlangen.de/FESTUNG.
Publications describing FESTUNG or showing its application are listed below:
- A preprint of the first paper, describing an older code version, is available from arXiv and we provide the codes described there as a gzip-archive.
- Our first paper FESTUNG: A MATLAB/GNU Octave toolbox for the discontinuous Galerkin method, Part I: Diffusion operator describes the basic data structures and discretization techniques.
The code corresponds to version 0.1 of FESTUNG. - Our second paper FESTUNG: A MATLAB/GNU Octave toolbox for the discontinuous Galerkin method, Part II: Advection operator and Slope Limiting describes the discretization of a hyperbolic operator and slope limiting techniques.
The code corresponds to version 0.2 of FESTUNG.
A preprint of the paper, describing code version 0.2-beta.1, is available on arXiv. - Our third paper “FESTUNG: A MATLAB/GNU Octave toolbox for the discontinuous Galerkin method, Part III: Hybridized discontinuous Galerkin (HDG) formulation” (submitted to CAMWA).
A preprint of the paper, describing code version 0.3-beta.1, is available on arXiv. - A poster at SIAM Geosciences 2017 outlining the features and concepts of FESTUNG.
Data visualization
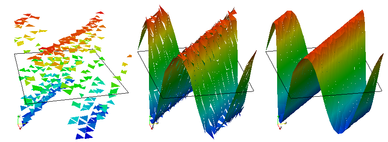
FESTUNG writes VTK- and Tecplot-files with the computed solution that can be visualized, e.g., using Paraview or Tecplot 360.