UTBEST3D
UTBEST3D (University of Texas Bays and Estuaries Simulator — 3D) |
||||||||
|
UTBEST3D (University of Texas Bays and Estuaries Simulator — 3D)
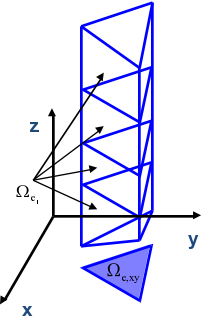
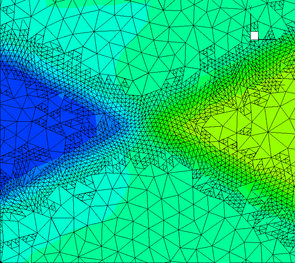
The numerical solution algorithm in UTBEST3D considers the system of hydrostatic primitive equations (1) with a free surface. A prismatic mesh (Fig. 1) is obtained by projecting a given triangular mesh in the vertical direction to provide a continuous piecewise linear representations of the topography and of the free surface. The vertical columns are then subdivided into layers. If a bottommost prism is degenerate, it is merged with the one above it. Due to the discontinuous nature of the approximation spaces, no constraints need to be enforced on the element connectivity. Hanging nodes and mismatching elements are allowed and have no adverse effects on stability or conservation properties of the scheme. This flexibility with regard to mesh geometry is exploited in several key parts of the algorithm: vertical mesh construction in areas with varying topography (Fig. 4), local mesh adaptivity (Fig. 2), wetting/drying (Fig. 3).
\partial_t {\bf u}_H +\nabla \cdot \left( {\bf u}_H {\bf u} – D_{\bf u} \nabla{\bf u} \right) + \nabla_H P -f_C {\bf k} \times {\bf u}_H =0
\partial_t T + \nabla \cdot \left({\bf u} T – D_T \nabla T \right) = 0
\partial_t S + \nabla \cdot \left({\bf u} S – D_S \nabla S \right) = 0
\partial_t \xi + \nabla_H \cdot \int_{z_b}^{\xi} {\bf u} dz =0\hspace{45mm}(1)
\nabla \cdot {\bf u} =0
\partial_z P= – \frac{\rho}{\rho_0}g
\rho = \rho(T,S,z)
\nabla_H = (\partial_x,\partial_y), {\bf k} = (0,0,1)^T, D_{X, X \in \{{\bf u},S,T\}} – eddy viscosity/diffusivity, \xi – free surface elevation, z_b – bathymetry, {\bf u}= (u,v,w) – velocity, {\bf u}_H= (u,v), T – temperature, S – salinity, P – pressure, \rho – density, \rho_0 – reference density, g – gravity acceleration, f_C – Coriolis coefficient.
Our DG discretization is based on the local discontinuous Galerkin method (Cockburn, Shu, 1998) that represents a direct generalization of the cell-centered finite volume method, the latter being just the piecewise constant DG discretization. One of the features of this method is a much smaller numerical diffusion exhibited by the linear and higher order DG approximations compared to the finite difference or finite volume discretizations. The method guarantees the element-wise conservation of all primary unknowns including tracers, supports an individual choice of the approximation space for each prognostic and diagnostic variable, demonstrates excellent stability properties, and possesses proven local adaptivity skills (Fig. 2).
UTBEST3D is written in C++ to provide clean interfaces between geometrical, numerical, computational, and communication parts of the code. The object-oriented coding paradigm is designed to enable a labor efficient development lifecycle of the model. The programming techniques were carefully chosen and tested with the view of guaranteeing a smooth portability to different hardware architectures, operating systems, compilers, and software environments; the package relies on no external libraries in the serial configuration and only makes use of METIS (Karypis, Kumar, 1999) grid partitioning library in the parallel configuration.
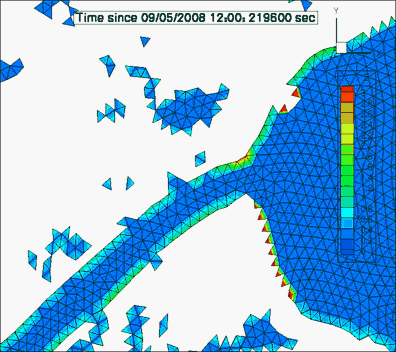
Wetting/drying simulation of a storm surge during hurricane Ike. Visible fractionally subdivided elements at the wet/dry interface.
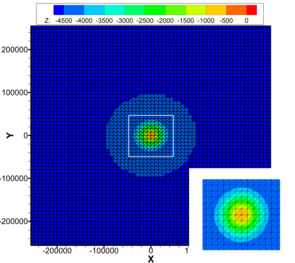
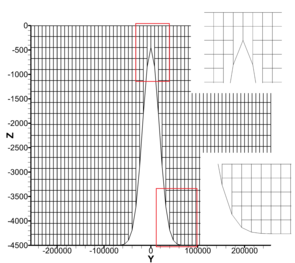
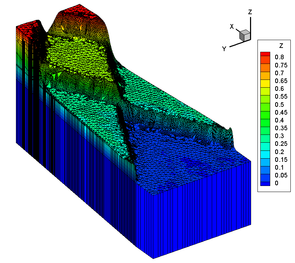
Geometry and mesh of the steep seamount test case. Bathymetry and horizontal mesh, vertical mesh.
Bibliography
- Vadym Aizinger, A discontinuous Galerkin method for two- and three-dimensional shallow-water equations, PhD Dissertation, THE UNIVERSITY OF TEXAS AT AUSTIN, 2004.
- V. Aizinger, C. Dawson, The local discontinuous Galerkin method for three-dimensional shallow water flow, Computer methods in applied mechanics and engineering, 196, 734-746, 2007.
- B. Cockburn and C.-W. Shu, The local discontinuous Galerkin method for time-dependent convection-diffusion systems, SIAM J. Numer. Anal. 35, 2440-2463, 1998.
- C. Dawson, V. Aizinger, A Discontinuous Galerkin Method for Three-Dimensional Shallow Water Equations, Journal of Scientific Computing, 22, 245-267, 2005.
- G. Karypis and V. Kumar, A fast and high quality multilevel scheme for partitioning irregular graphs, SIAM Journal on Scientific Computing, 20(1), 359-392, 1999.