Master’s theses

Multiscale Elasto-dynamics

Description

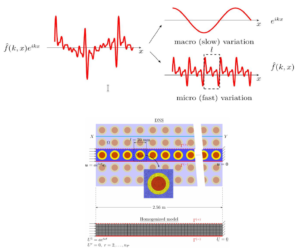
Now a days, considerable progress is being made in the design of composite materials which can exhibit properties that are not found in naturally occurring materials. Numerical homogenization techniques are used in order to find effective properties of periodic microstructures at the macro-scale. In conventional homogenization methods, the material properties are averaged over a repeating Representative Volume Element (RVE) in order to calculate those effective properties. But in the case of elastodynamics, uniform volume averaging can lead to a loss of phase information which is necessary to accurately describe the elastodynamic material at the macro-scale. Such limitations can be overcome by transferring the microscale information to the fourier space and then projecting the frequency modes to a reduced space composing a few selected Floquet-Bloch eigenmodes, thereby reducing the degrees of freedom at the macro-scale. The homogenized parameters can then be utilized in a material optimization
setting, thus optimizing the dynamic properties of the structure.

“A general multiscale framework for the emergent effective elastodynamics of metamaterials” – A. Sridhar, V.G. Kouznetsova, M.G.D. Geers

Objective

To develop a multiscale method for elasto-dynamic simulation using homogenization in the fourier domain.

Prerequisites

Good knowledge of numerics of partial differential equations, mathematical optimization, programming in MATLAB/Python/C++ and a lot of enthusiasm.
Language: English or German

Tasks

• Literature research
• Model development
• Numerical experimentation
• Writing Thesis and dissemination of the results.

Optimization of a Mechatronic Sensor

Maximizing the sensitivity and robustness of a mechatronic sensor through structural optimization.
In cooperation with a regional industry partner.

Tooth Root Optimization

Topology optimization of a tooth root. Attempt to compare evolution against structural optimization. For CE students who aren’t afraid of the dentist. 🙂

Solar air heater

Solar air heaters are fascinating simple, cheap and efficient devices for environmental friendly ventilation and heating. Yet, solar air heaters are widely unknown in western countries.

Based on an existing numerical setup for a coupled flow/heat model, certain properties can be structurally optimized by means of gradient based optimization.

HiWi jobs

We are constantly looking for dedicated students starting from Bachlor level to work on small scientific projects in our group. If you are interested in optimization, numerics and challenging applications and have some income on a regular base, please contact us. For students of mathematics and computational engineering.