Research
Research at the Chair of Applied Mathematics III
The Chair of Applied Mathematics III belongs to the Section Modeling, Simulation and Optimization of the Department of Mathematics. Our research groups is positioned in the domain of Scientific Computing. Important focal points of interest are flow simulation and image processing.
Flow simulation

Although we do not always think of it, flows surround us and determine our lives. Examples are weather and climate, and, on a smaller scale, blood flow through arteries or air flow through our lungs. Simulation of such flows is of major interest, as we experience, for example, when looking at the daily weather report.
Of course, flows appear also in many technical areas. Examples are: Flow around vehicles, accoustics, hydraulic phenomena, etc.
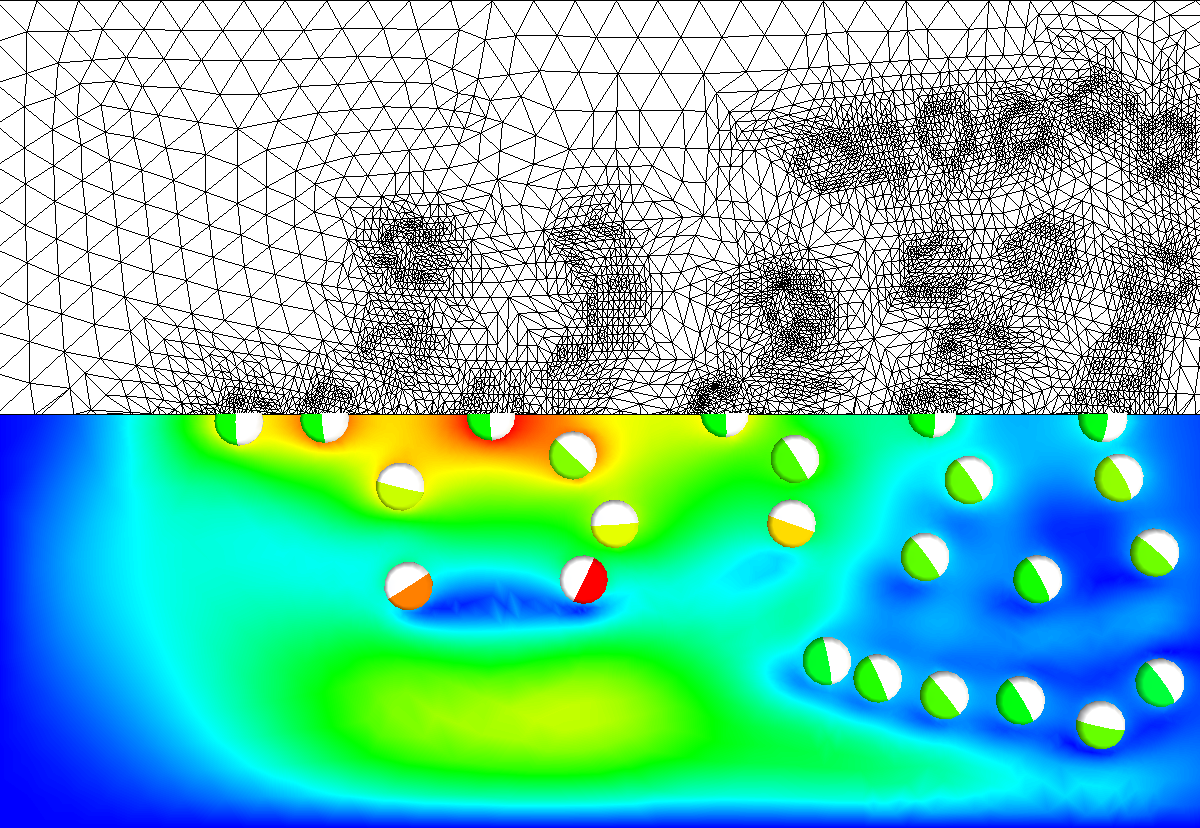
The importance of simulations lies in the fact, that it can replace expensive experiments, and that it can even look into a physical quantities which are not (or only very difficult) accessible experimentally. Examples are parameter studies in climate research for future climate development, or research in medicine.
Common to all flows is that they can essentially be described by the so-called Navier-Stokes equations, which are a both interesting and difficult system of partial differential equations. Differences between flows like compressible/incompressible, viscous/nonviscous, etc reflect in parameters of these equations.
Finally, we remark that flow simulation is a vibrant field of interdisciplinary research, in which mathematicians work together with engineers, physicists, and computer scientists.

