PDE-restricted Optimization
PDE-restricted Optimization
|
EWave – Energy management water supply (2014-2016) The EWave project is concerned with the development of an decision support system for energy optimal management of water supply systems. At the moment, water supply is oriented towards security of supply. Based on increasing energy costs the BMBF-research program EWave has the goal to improve the energy efficiency of water supply. Therefore an energy management system should be developed. This system should be applied and tested at a water company for the first time. In the first step, it should serve as strategic planning tool for the plant management. It should be possible to examine basic considerations of the “plant operation mode” which should be used as short-term operating instructions. In a second step it is intended to use it as an operative decision support system. In the development of such an energy management system, various mathematical problems occur. First, a mathematical description of the supply network has to be modeled. On the one hand, the flow of water in the pipes is simulated. On the other hand, the systems of water treatment and distribution must be included in the model. An adequate modeling of these aspects leads to a high-resolution model of the water supply network. Partners in industry: Siemens AG, RWW und GreyLogix Aqua GmbH
|
|
Prof. Dr. Günter Leugering (Erlangen), Dipl.-Technomath. Maximilian Walther (Erlangen) |
|
OPAL – Optimization of Airlay Processes (2013-2016) The project OPAL, split into five sub-projects at FAU Erlangen, TU Kaiserslautern and Fraunhofer ITWM, investigates the industrial process of manufacturing nonwoven materials including the single fiber traveling in turbulent air flow, laying down onto a ramp of loosely connected fibers and finally forming networks being glued together by thermal bonding. This particular subproject is concerned with the resulting micro structure, its mechanical properties and optimization.
Finally the nonwoven textile is to be optimized regarding its effective mechanical properties, like toughness, insulation properties etc. This can be done by theoretical considerations regarding the particular structure of the RVE, for example moving nodal points where fibers meet freely in space to obtain optimal micro structures. These optimized structures then define a theoretical upper bound for an optimization taking into account the whole laydown process. In order to get closer to this scenario, parameters of stochastic nets have to be identified which determine the macroscopic behavior, so that the process can be controlled by steering into regions of optimal parameter sets.
|
|
Prof. Dr. Günter Leugering (Erlangen), Dipl.-Technomath. Christoph Strohmeyer (Erlangen) |
|
Shape optimization of nanoantennas (2012-present) One aim of this project is the application of shape optimization on nanoantannas and nanooptical circuits to enhance its efficiency. By experiments one can see that the shape of a nanoantenna influences its efficiency. Optical nanoantennas are attached to waveguides to couple a laser beam into a nanooptical circuit. By experiments one can see that the shape of a nanoantenna influences its efficiency. Efficiency in this particular case is the ratio between energy of the laser beam and gained energy in the waveguide. Light is described by electric and magnetic fields, and their propagation is modelled by Maxwell’s equation. If time-harmonic fields are assumed, Maxwell’s equation is reduced to its time-harmonic representation. |
| Prof. Dr. Günter Leugering (Erlangen), Prof. Dr. Ulf Peschel (Erlangen), Johannes Semmler MSc. (Erlangen), Dipl.-Phys. Arian Kriesch (Erlangen) |
|
Optimization of iron oxide Pigments (2012-2017) The dependency of the optical properties of a pigment film and the shape or shape distribution of the pigment is studied within this project. Further, this dependency is used to identify regions in parameterized shape space which will lead to better color values of the pigment. Details The interaction of electromagnetic waves and material is mathematically described by Maxwell’s equations. Under the assumption of a time-harmonic incident light – which holds in the studied regime – this equations can be transformed to the well known curl-curl formulation of Maxwell’s equation. |
| Prof. Dr. Günter Leugering (Erlangen), Prof. Dr.-Ing. Wolfgang Peukert (Erlangen), Prof. Dr. Ulf Peschel (Erlangen), Prof. Dr. Robin N. Klupp Taylor (Erlangen), Dr. Lukas Pflug (Erlangen) |
|
LeOpIn – Lebenszyklusoptimierung (2010-2013) The LeOpIn project (lifecycle oriented optimization for ressource and energy efficient infrastructure) is concerned with the design of energy efficient office buildings and piping systems in power plants. Details LeOpIn consists of six subprojects, where three are located at the chair of Applied Mathematics 2. In the planning phase of large construction projects typically just the investment costs are considered. In the present feasibility study however the whole life cycle of buildings/piping systems is taken into account. This way, aspects like accumulated carbon footprint as well as sustainability can be integrated to a large extend into the decision making. The structure of LeOpIn can be illustrated on the case study of high-pressure piping systems: After modeling the system physically accurate, the describing models have to be prepared by means of model reductive techniques for a subsequent optimization. When modeling high pressure pipes it is essential that besides capturing static and dynamic behavior of steel tubes longtime material properties are described. To this end different beam models which describe thin one dimensional structures are coupled with various material models like thermo elasticity, plasticity and creep damage. The resulting highly nonlinear partial differential equations can be solved by computers utilizing numerical methods. Partner in industry: Bilfinger SE |
| Prof. Dr. Günter Leugering (Erlangen), Prof. Dr. Michael Stingl (Erlangen), Dipl.-Technomath. Tobias Kufner (Erlangen), Dipl.-Technomath. Christoph Strohmeyer (Erlangen), Dipl.-Technomath. Maximilian Walther (Erlangen) |
|
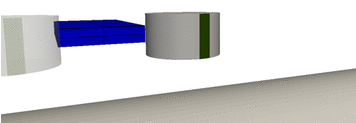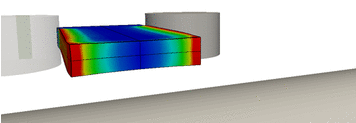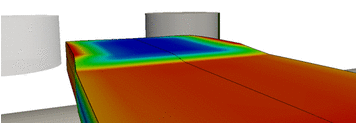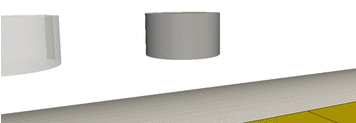
Model-Based Control of Slab Shapes in Hot Rolling Processes (2010-2013) We want to minimize unnecessary manufacturing costs arising in hot rolling processes by solving an optimal control problem that uses the trajectories of the rolls as control functions. We consider hot rolling processes, in which a metal solid body is deformed by several rolls in order to obtain a desired final shape. To minimize the cutting scrap and to ensure at the same time that this shape satisfies the required tolerances as accurately as possible, we formulate an optimal control problem where we use the trajectories of the rolls as control functions. The associated constraints defining the admissible set of the problem result from industrial specifications and technical limitations.
The motion and deformation of a solid body subject to different external forces can be described through the basic equations of nonlinear continuum mechanics, which are here coupled with an elasto-viscoplastic material model. This model is based on a multiplicative split of the deformation gradient into elastic and plastic parts and specifies the behavior of metals at high temperatures and high rates of deformation. Since we moreover assume that we can neglect the deformations of the rolls, we also have to add unilateral frictional contact boundary conditions and therefore end up with an evolutionary quasi-variational inclusion as weak form of the state problem. |
| Prof. Dr. Günter Leugering, Prof. Dr. Michael Stingl, Dr. Stefan Werner |
|
Control of System Dynamics in Gas and Water Networks (2009-2012) The dynamics in gas or water networks are governed by the isothermal Euler equations or the Saint Venant equations (shallow water equations), respectively, which form hyperbolic balance laws. For these networks we analyse (optimal) control and stabilization problems as well as the numerical application of the theoretical results. Efficient control of gas and water transportation networks plays an important role in industrial and municipal supply as well as in flood management. The gas flow through pipes can be controlled via compressors and valves, the water flow in canals can be controlled via pumping stations and flow gates. The picture shows a part of a compressor station (source: WINGAS). The dynamics in gas or water networks are governed by the isothermal Euler equations or the Saint Venant equations (shallow water equations), respectively, which form hyperbolic balance laws. For these networks we analyse (optimal) control and stabilization problems as well as the numerical application of the theoretical results. This project is a cooperative project between the RWTH Aachen University and the Friedrich-Alexander-University Erlangen-Nuremberg and is funded by the DFG Schwerpunktprogramm 1253. |
| Prof. Dr. Günter Leugering (Erlangen), Prof. Dr. Martin Gugat (Erlangen), Dr. Markus Hirsch-Dick (Erlangen), Prof. Dr. Michael Herty (Aachen) |
|
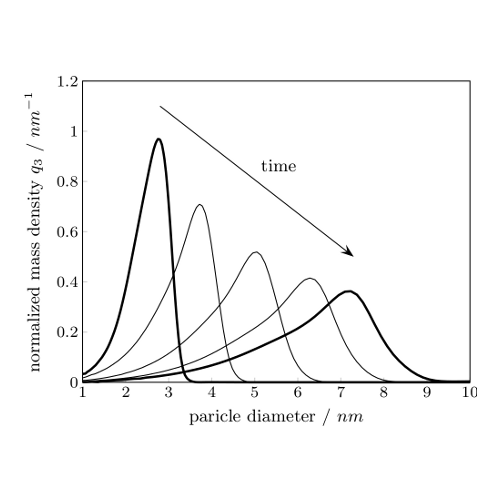
Optimization of Particle Synthesis The economic production of nanoscaled particulate products with exactly pre-defined characteristics is of enormous relevance. Although there are different particle formation routes they may all be described by one class of equations. The economic production of nanoscaled particulate products with exactly pre-defined characteristics is of enormous relevance. Although there are different particle formation routes they may all be described by one class of equations. Therefore, simulation of such processes comprises the solution of nonlinear, hyperbolic integro-partial differential equations. This project aims to study this class of equations in order to develop efficient tools for the inverse solution, i.e. determining the optimal process conditions to achieve a desired product property. |
| Prof. Dr. Günter Leugering (Erlangen), Prof. Dr.-Ing. Wolfgang Peukert (Erlangen), Dr. Michael Gröschel (Erlangen) |
|
Multiscale optimization of a composite material concerning crack resistance The final aim of the project is to determine different parameters for a composite material in an optimal way so that it exhibits desired properties concerning the growth of cracks. The final aim of the project is to determine different parameters for a composite material in an optimal way so that it exhibits desired properties concerning the growth of cracks. To start with crack growth on the micro scale is studied, which can be influenced by parameters on the micro scale as well as by parameters on the atomistic scale (cohesive laws). The project includes on the one hand the development of an efficient simulation method for crack growth handling various phenomena like crack kinking and branching and paying attention to cohesive effects. Therefore the crack problem is formulated as an energy minimization problem and is studied in mathematical detail. On the other hand optimization problems, which cover for example the optimization of shapes of fiber inclusions, are formulated mathematically and solved numerically. Later on homogenization techniques will allow for getting one step higher on to the macro scale so that one can aim for application of multilevel optimization techniques over three different scales. |
| Prof. Dr. Günter Leugering (Erlangen), Prof. Dr. Michael Stingl (Erlangen), Prof. Dr.-Ing. Paul Steinmann (Erlangen), Prof. Dr. Alexander Hartmaier (Bochum), Dr. Marina Prechtel (Erlangen) |




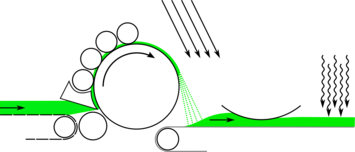
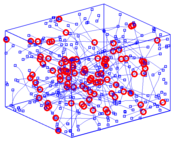 The inner structure of the fiber network determines effective material properties of the nonwoven textile. On the micro scale stochastic fiber networks have to be tackled, both from a modeling and a numerical point of view. The fibers are modeled by different beam models: linear Timoshenko beams and geometrically exact beams, which both allow for shear deformation but differ in mathematical complexity. In order to compute effective properties two strategies are pursued: direct numerical simulation of a representative small part of the nonwoven (RVE) and homogenization, where the microscopic structure is being dropped and the textile is described by a different homogenized model.
The inner structure of the fiber network determines effective material properties of the nonwoven textile. On the micro scale stochastic fiber networks have to be tackled, both from a modeling and a numerical point of view. The fibers are modeled by different beam models: linear Timoshenko beams and geometrically exact beams, which both allow for shear deformation but differ in mathematical complexity. In order to compute effective properties two strategies are pursued: direct numerical simulation of a representative small part of the nonwoven (RVE) and homogenization, where the microscopic structure is being dropped and the textile is described by a different homogenized model.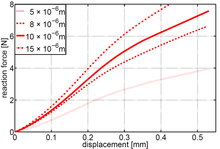




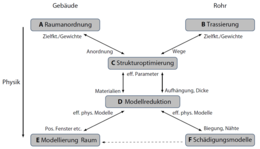
 Thereby, a newly developed algorithm exploits the network structure of the pipeline and creates an effective overall model.
Thereby, a newly developed algorithm exploits the network structure of the pipeline and creates an effective overall model. The case study of office buildings can be treated in a similar way – from a mathematical point of view both physical systems can be seen as graphs. This way the methods for model reduction and optimization algorithms may also be used for planning and optimizing buildings. Solely the underlying physical model has to be developed separately.
The case study of office buildings can be treated in a similar way – from a mathematical point of view both physical systems can be seen as graphs. This way the methods for model reduction and optimization algorithms may also be used for planning and optimizing buildings. Solely the underlying physical model has to be developed separately.